21 Dec 2017
Paper Notes: The Case for Learned Index Structure
前几周看了Jeff Dean在Nips17上演讲的Slides,其中提到一些有趣的工作,包括最近在网络媒体上出现次数比较多的这篇文章The Case for Learned Index Structure。周末仔细读了一遍,来分享一下思路和具体细节。
有没有想过用机器学习的方式解决系统设计中的问题?这是个蛮有趣的命题,它的难点在哪儿呢:系统里的算法或数据结构往往是确定性的,显式的(我们清楚地知道输入和输出间的映射关系),而机器学习中的模型是依赖于输入数据训练出来的(下文会看到事实上数据结构的建立也是依赖于数据的),并且存在一定的误差(而很多时候系统模块有严格限制条件)。虽然在系统设计时应该考虑所有(最坏)数据的情况,但是在做系统优化的时候,通常会通过一些特殊性来对系统做特定的设计。这里的特殊性包括数据特殊性和使用特殊性。数据特殊,比如对给定范围且没有重复的数组排序,可以直接用bitmap。使用特殊,例如由于业务场景,读写比例相差很多(每周只更新一次),实现某种数据结构的时候可以把读实现成O(1),写实现成O(n),而标准实现往往是在保证均摊最优情况下让各操作复杂度尽量接近,因为假设各操作使用频率相近。而大多数时候只可能知道使用特殊性,却很难知道数据的特殊性。这里很自然的思路就是通过数据训练出一个机器学习的模型(由于多层神经网络的泛化能力这里考虑神经网络模型)去encode这种特殊性(如果存在),然后对比看看用这个模型是不是能有些优势,如缩短计算映射的时间,减少存储等等。当然,如果这种映射关系能被人理解,也可以更好地去实现系统模块。
这篇paper就试图用这个想法去优化索引 (Index) 问题。首先,索引的过程本身就是模型:Range Index索引可以看做是从给定key到一个排序数组position的预测过程,Point Index索引可以看做是从给定key到一个未排序数组的position的预测过程,Existence Index索引可以看做是预测一个给定key是否存在(0或1)。这样一来,索引系统是可替换的,我们可以直接用ML模型去替换现有的索引模块实现。其次,数据特殊性对索引设计的影响明显。假设用于Range Index的key的范围是1-100M,那么可以用特殊的hash函数(直接把key本身当成是offset)去做索引而不必再用B-Tree。然而,用ML模型去做索引也可能存在一些问题:
- Semantic Guarantees. 通过数据训练得到机器学习的模型是存在误差的,但是我们设计的索引经常需要满足严格的限制条件。举例来说,bloom-filter的优势之一是可能会有把不存在的错判成存在(False Positive)但绝不会把存在的错判成不存在(False Negative)。
- Overfitting. 如果避免模型的overfitting?换句话说,如果当前训练的模型只能memorize当前数据形态而并不能generalize新的数据,该怎么办?
- No Specialization. 如果数据并没有任何特殊性,如完全随机或者不能被我们的设计模型架构所归纳,该如何处理?另一种情况是,新的数据破坏了之前模型归纳出的特殊性,比如新的数据来源于一个新的或者是变化了的distribution。
- Evaluate Efficiency. 模型的inference过程相比显式索引数据结构的计算更昂贵。
顺着上面的思路,带着这四个问题,具体来探索一下数据库系统中的三类索引:Range Index ,Point Index和Existence Index。
Range Index. 数据库系统通常使用B-Tree或B+-Tree来实现range index。查询时给定一个key(或一些定义range的keys),B-Tree会索引到包含该key的对应范围的叶子节点,在叶子节点内对key进行搜索。如果该key在索引中存在,就会得到其对应的position。这里position代表指向逻辑页的一个offset或pointer 。一般在一个逻辑页内的records会用一个key来index。如图所示,输入是一个key,输出是对应要查询record的position的区间[pos, pos + pagesize]。
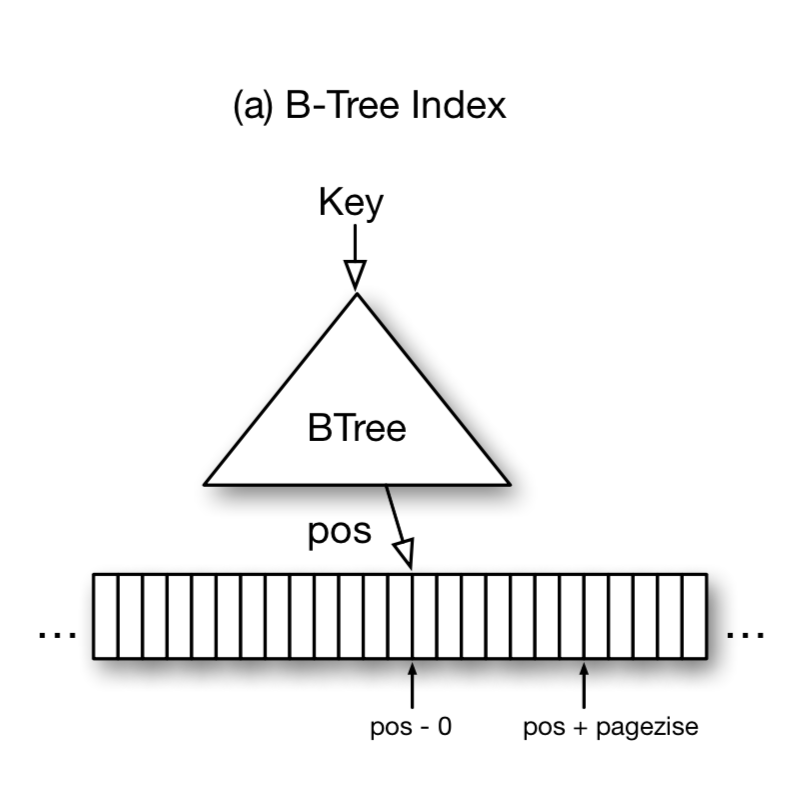
有趣的是,在机器学习的观点下,B-Tree索引实际上可以看成是一个regression tree模型,这个模型(B-Tree)的建立过程也是依赖数据的,只不过它不是通过梯度下降的方式得到的,而是通过预先定义的法则(insert函数)。如下图2,对于输入x,模型预测出一个pospred,若区间pospred - minerr, pospred + maxerr中包含这个record,那么预测准确,其中minerr的期望是0(这时pos就是record的位置),maxerr的期望是pagesize(这时record的位置在pos+pagesize)。那么minerr和maxerr在模型中具体如何计算呢?对于训练数据(现有的(key,pos)),计算出每一组pospred和和pos的正负差,然后取最大的正差就是maxerr,负差就是minerr。这里并不需要考虑不在索引中的key,因为B-Tree本身也不能保证在新的key insert后搜索出来的pos和insert前的pos的差距在 \( [0, pagesize] \)(insert前B-Tree根本找不到这个key!)。
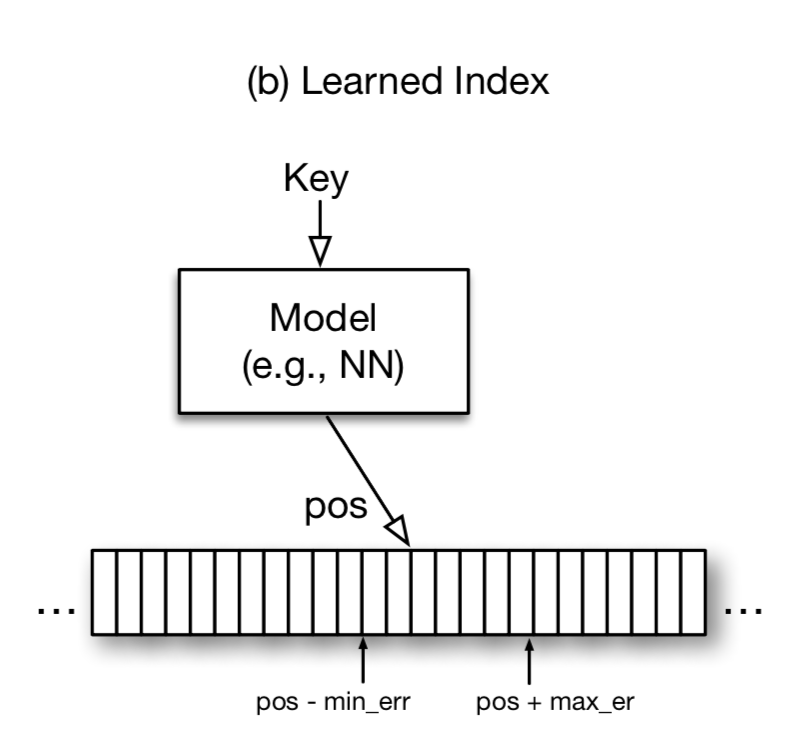
用图2的模型代替图1的B-Tree能否学到数据特殊性从而优化查询过程呢?假设有1M个key(取值从1M到2M),那么可以直接用一个等价关系(线性模型)代替B-Tree,也就能把log(n)的复杂度减少成常数复杂度。同样的,如果(key, pos)是一个抛物线,那么神经网络模型也可以通过常数复杂度进行预测。考虑到神经网络的泛化能力,如果数据具有特殊性,那么用模型代替B-Tree就能减少查询复杂度。具体B-Tree复杂度和神经网络模型复杂度的时间分析可以参考原文2.1。
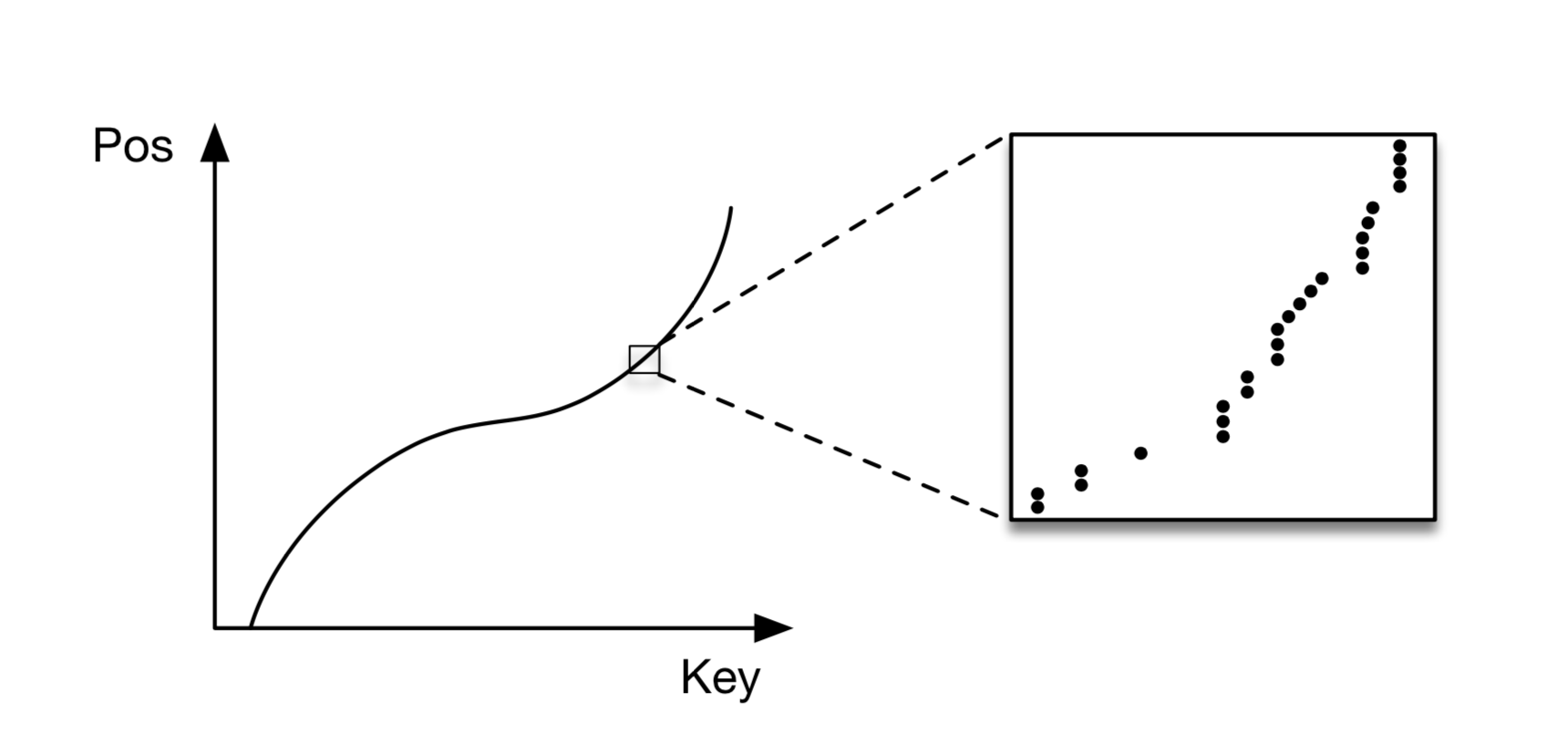
更进一步,还可以从概率的角度来思考range index这个问题。Range index实际上是描述一个数据点到一个有序数组的函数关系,也就是说这个函数关系"模拟"出了数据的累计分布函数(CDF)。因此,可以这么来定义这个函数:\( p = CDF(key) * N\) ,其中p是position,CDF(x)是 \( Prob(X <= key)\),N是所有的key的总数。CDF函数可以简单理解成一种描述概率函数的wrapper函数,它描述随机变量X在小于一个key条件下的概率和。有了CDF,就能很容易地描述一个区间X的概率和:\( CDF(key2) - CDF(key1) = Prob(key1 <= X <= key2)\),它能够帮助进一步深入地研究概率分布理论。这么来理解此处的"模拟"就明白了:假设我们把pos和key的函数关系写成\(p = F(key) * N\),其中F是一个任意函数。那么F满足以下性质: $$设p1 = F(key1) * N和 p2 = F(key2) * N$$ $$p1 - p2 = (F(key1) - F(key2)) * N = F(key1 - key2) * N$$ 最后这个等式由range index满足,因为range index映射到的pos是一个在有序数列里。而巧合的是累计分布函数(CDF)也满足这个性质。虽然满足这个性质的函数不一定要是CDF,但是如果能把一个更强假设的函数(CDF)学习出来,那么一定也满足range index的功能!使用这个更强假设(CDF)的好处是:拟合数据的CDF函数是一个active的研究方向,可以受益于已有的研究成果。
基于这个想法,让我们先抛开拟合CDF,尝试用一个简单的两层全连接神经网络(每层32个neurons + ReLU acitivation)训练了一个200M的web-server log records,x是timestamp,label是对应B-Tree索引到的position。并测试了用训练得到的模型的预测时间,latency大约是80000 ns,throughput是每秒1250次预测。很遗憾,这比不用索引遍历还要慢。然而B-Tree的索引时间大概是300 ns。那么问题出在哪儿呢?首先,这里用了Tensorflow做训练和预测,Tensorflow是位较大规模的神经网络做的优化,但并不适用于这里的小网络,并且python层因为用swig做胶水层会造成一定的latency开销。其次,机器学习中的树模型(比如B-Tree模型)能够更好地记住数据特征,因为它能不断的split data space。而这里用的神经网络模型能够很快地学习出一个做地还不错的模型,但是很难做到局部数据上的准确(这里可以用overfitting来理解)。为了保证精度,我们要train更多的epoch,并且使用更深的网络来训练。这里还有一个原因导致需要用更深的网络来尽量达到树模型的精度:训练目标不仅要降低每个预测position和label间误差的平均,更重要的是要让训练出来模型的minerr和maxerr尽量小,也就是让预测出来的position在真正的page内(注意这里并没有把minerr和maxerr加到优化函数里,而只是假定预测精度越小,这两err越小)。同时,B-Tree是cache-efficient的:能把很少的上层节点放入cache。而对于全连接神经网络模型,要把模型都加载到内存,并且权重不是稀疏的!
为了尝试解决以上的问题,文中首先提出了Learning Index Framework(LIF)。LIF就是一个索引优化系统,给定一套索引数据,LIF自动生成多组超参数,并且自动地优化并测试,找出最优的一组配置。训练时,LIF任然用了TensorFlow,而在inference时LIF根据训练打包的模型,用code-generation(用特定的模型结构减少运行时开销,比如剪枝、去掉多余的if-else、direct memory access等,这里不展开。如果对数据库系统了解的同学应该比较熟悉)自动生成了相应C++的程序,这里实现具体的细节可以参考21。这样,可以把inference的开销减少到30 ns。
Recursive Model Indexes(RMI). 既然LIF可以在很短的时间里完成预测,我们就可以考虑用更复杂的模型来尝试替换B-Tree索引了。上文提到,单个全连接网络并不能达到很好地准确度。事实上,如下图所示,全连接神经网络模型虽然可以从整体上较好地拟合出整体数据分布,但由于每个数据个体本身的随机性,却很难同时在局部也准确拟合出个体数据,文中把这个问题称作the last-mile accuracy问题。换句话说,对于一个100M条记录的数据集,我们可以先用单个简单的模型把误差控制在10K并不困难,然后对于局部数据,再用另外的模型进行预测把误差从10K降低到100。因此这里的思路就是用多模型来解决the last-mile accuracy问题,这里的多模型的思路并不是boosting,而是来源于混合专家网络(下文用MoE,可以参考51)。
MoE是90年代初提出的模型,下面先来介绍一下MoE模型的思想。真实情况下,数据往往来源于不同的概率分布,即使是单个概率分布也会随着时间变化。举个例子,比如股票价格,很难用一个连续的函数拟合分段函数(每天或每小时的变化曲线),也很难用一个分段函数去拟合一个连续函数(每月或每年整体的变化趋势曲线)。而如同上文所分析的,真实的数据分布函数往往是介于两者之间的:总体上满足一个变化趋势,但是局部却是分段函数(每天数据的分段函数可能都不同),因为这时随机因素更显著。MoE的想法是能否把数据partition,然后对于不同的数据,用不同的模型(称Expert)来进行拟合。这里需要特别指出的是,对数据本身的特征做partition并不一定能解决问题,而是应该根据不同的x和y之间的关系来对x做partition。
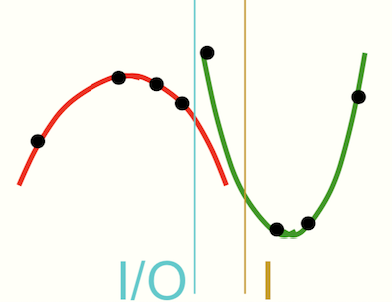
比如在上图的例子中,8个数据点来自两个抛物线,如果只根据数据本身做partition(右侧黄线),并不能很好地把数据partition在两个抛物线上,而左边的蓝线才是一个更好的parition。所以MoE的想法就是把x和y之间的关系定义到目标优化函数中,然后训练出不同的Expert来拟合不同的数据。如下图里,Gating Network可以认为是赋予每个Expert的权重,比如可以从输入接一个神经网络得到Softmax概率或Attention当成权重。然后对于这一个特定的输入,只训练在这个Attention下(或者Softmax较大概率)的Expert模型。换句话说,当某个Expert1表现比另一个Expert2好,反向传播时(y_pred - y更接近)Expert1对应Attention的权重就会更高,这样下去对于这个输入MoE就更加依赖于Expert1了。就好比小学一年级老师给大家一份数学卷子,学生A比学生B做的好,以后只要是数学题,老师都会重点培养A,让他成为一个数学特长生。而B可能更擅长语文,这就是MoE的基本思想。这里需要注意两点,不同于boosting,在预测时MoE对于不同的输入分配给各个模型的权重是不同的(softmax的概率或者attention)。而boosting一旦模型训练完成,在预测时分配给每个模型的权重是完全一样的。另一点,MoE有个很好的性质:虽然在训练的时候由于模型很多,参数也很多。但是在预测时候模型的参数并不随着模型复杂度的增加而增加,因此计算开销也不回增加,因为我们总是能Gating Network找出几个相应的Experts来做预测。这种稀疏性对于能够成功替换B-Tree索引至关重要!
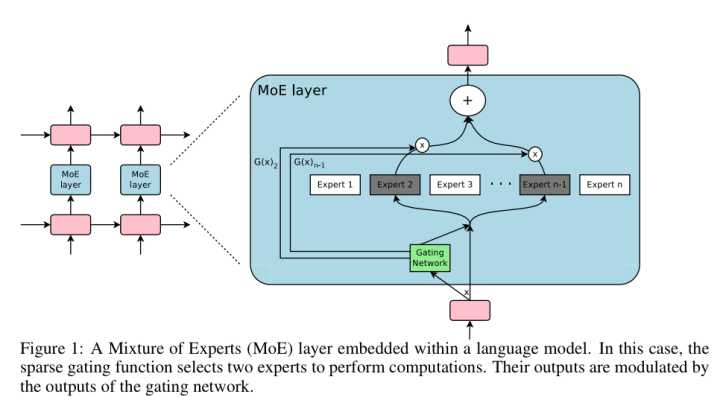
回到论文,文中提出了一种特定的MoE模型(文中称作Recursive Regression Model):RMI包含从顶到下M层,每一层包含 \( M_{l} \) 个Experts和一个Gating策略 \( M_{l} * f_{l-1}(x) / N \) ,每一层的Loss function是 \( L_{l}=∑_{(x,y)}(f^{M_{l}f_{l-1}(x)/N}(x) - y)^2 \) ,也就是说对于特定的(x, y),RMI委托特定路径的M个experts来对特定范围的x进行训练和预测,很好地解决了the last-mile accuracy问题。可以看到,这个MoE的特殊性在于,除了最下层的experts,其他层的所有experts的训练目标都是为了做Gating。我们可以看成是学一个attention(只有一个非零)的Gating Network,而只有最下层的expert才是做预测真正的experts。这里能这么假设的原因在于对于最下层,相近position范围内的数据分布一致(上一段提到我们通过x和y的关系来对x来做partition,这里通过除了最下层的所有experts层重新组织x来做这种partition使得在一个连续范围内的y的x被partition在了一起),用单个模型就够了(这里可以做进一步优化:在最下层前学出一个稀疏向量或者真正的attention)。需要注意的是,这里的分层模型并不是树,因为每个父节点也可能指向其他父节点的孩子。另外,在顶层expert可以用ReLU neural这种泛化表达能力更强但拟合性稍差的网络,而底层expert可以用拟合性更强的线性回归模型。
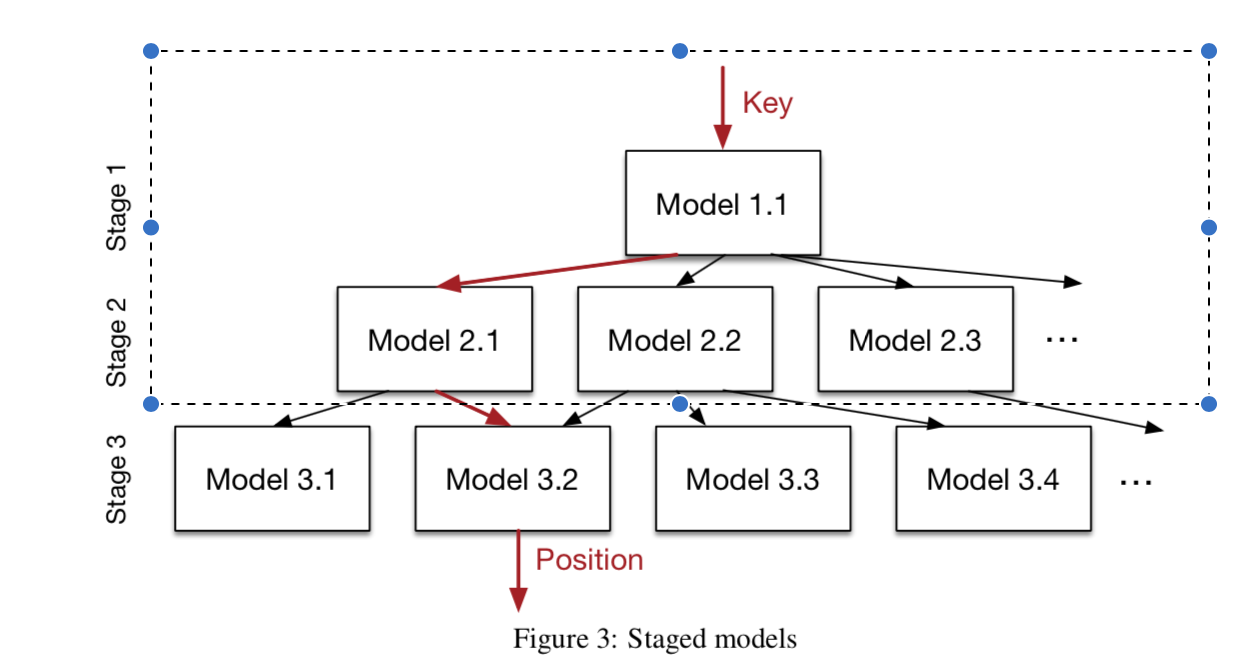
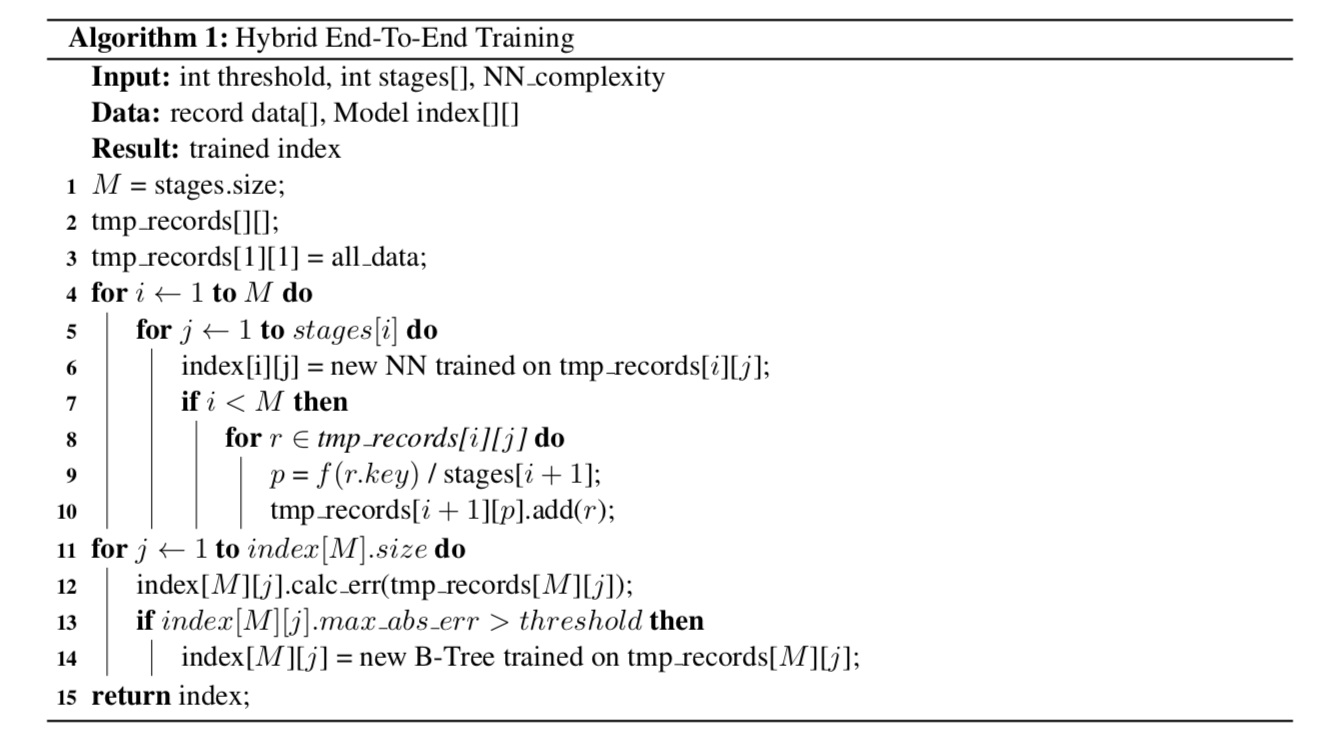
本文开始提到No Specialization的问题:如果数据本身是随机的,RMI模型并不能归纳出数据中的分布规律,应该怎么办?这里的思路就是rollback到B-Tree Index(下文会看到对于Point Index和Existence Index都会有类似处理来解决No Specialization问题)。由于RMI模型的稀疏性和LIF的高效率,即使对于这种情况,加入RMI的range index效率也并不会降低太多。整个训练过程见下图,文中是分stage训练的(也可以用end-to-end),训练时可以用grid search和一些best practice来tuning hyper-parameter。我们知道,在训练完RMI后,能得到每个experts的minerr和maxerr。我们可以用它们来和预先给定的threshold(比如设成pagesize)对比,当成rollback的条件。更重要的是,它们能够优化索引搜索过程。通常的B-Tree在找到输入key的offset后会用binary search(也有其他的方式如Quaternary Search但是效率提高不明显)。而RMI模型预测出来的position可以用作更准确的pivot来进一步提高搜索record的性能。论文中提出了Model Binary Search,Biased Search和Biased Quaternary Search,这部分比较简单,就不展开说了,可以参考论文3.4。
论文中用了四个数据集来做了实验,分别是Weblogs(日志数据,用timestamp建索引,这个最符合真实复杂环境), Maps(地图数据用经度建索引,虽然这个也是真实数据,但是相对更规则), Web-documents(真实的document数据)和合成的Lognormal(采样生成的数据,为了模拟真实环境中的长尾分布)。其中Weblogs、Maps和Lognormal数据使用整数来当索引的,而Web-documents是用字符串来当索引的(因为不连续)。下面分别列出了四组数据的实验效果。在每组数据集的实验中,论文以pagesize=128作为baseline,分别给出了Learned Index与B-Tree Index索引时间(Model列表示搜索position的时间+Search列表示搜索record的时间)的对比、索引内存占用的对比以及索引误差。在最后一组Web-document数据的实验里,文中对比了不同的搜索策略,因为对于string的binary search会更耗时,所以上文提出的搜索策略能够更明显地提高效率。这里Learned Index只用了两层的RMI,Learned Indexed Complex表示第一层用了两层全连接的网络,而不带Complex的没有用hidden layer。而第二层都使用了linear model,论文对第二层里不同的experts数目做了不同的实验。
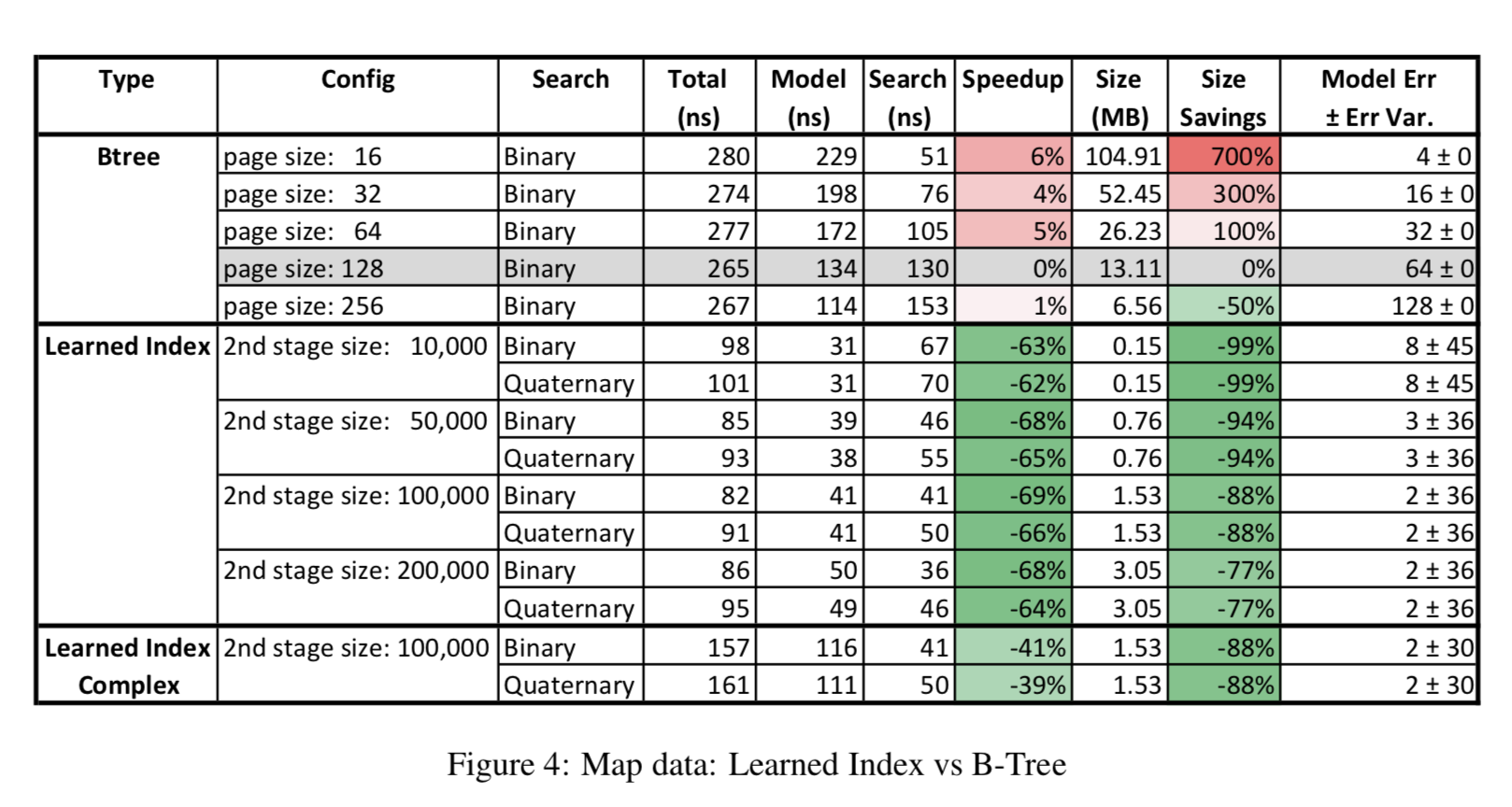
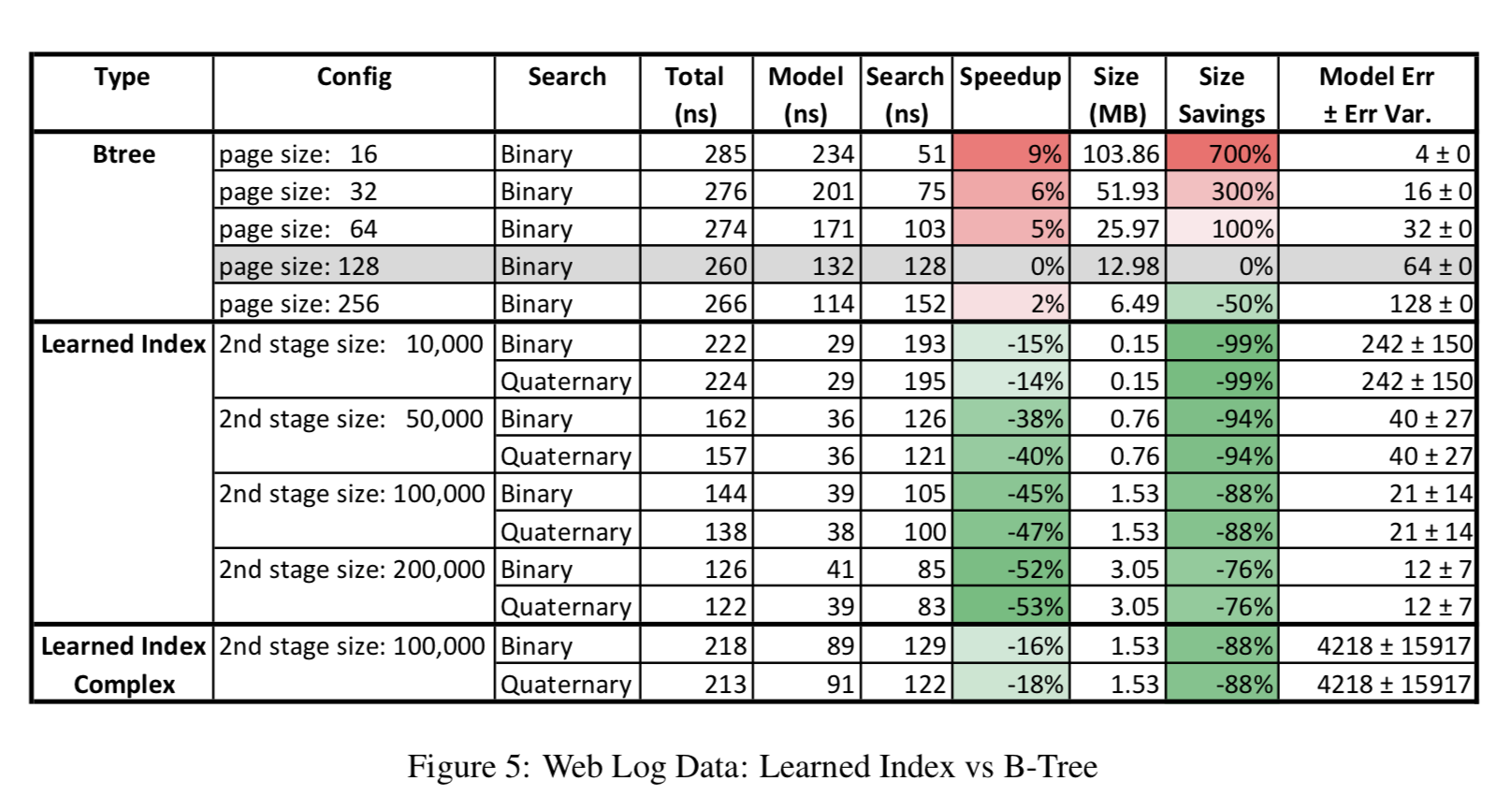
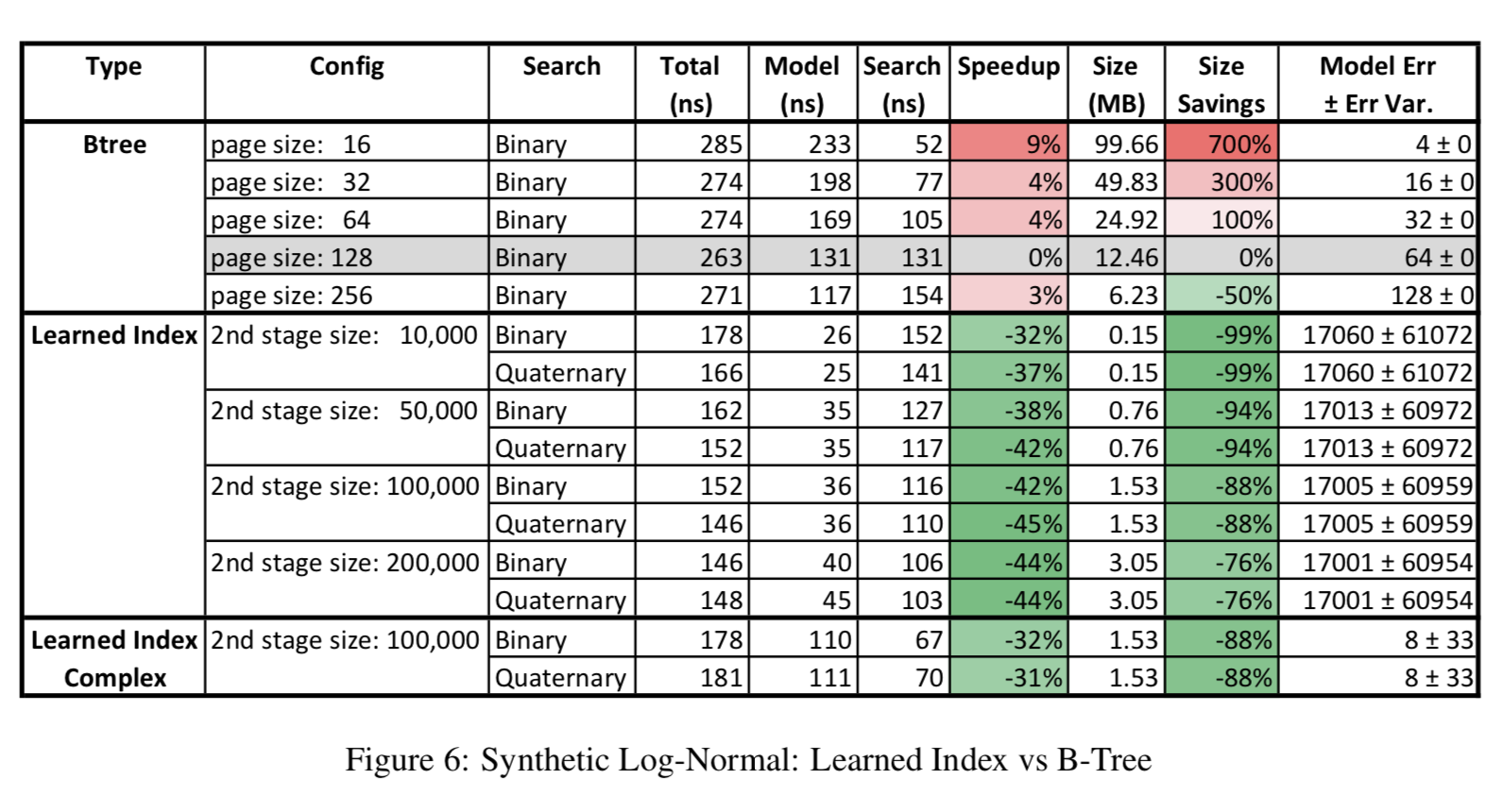
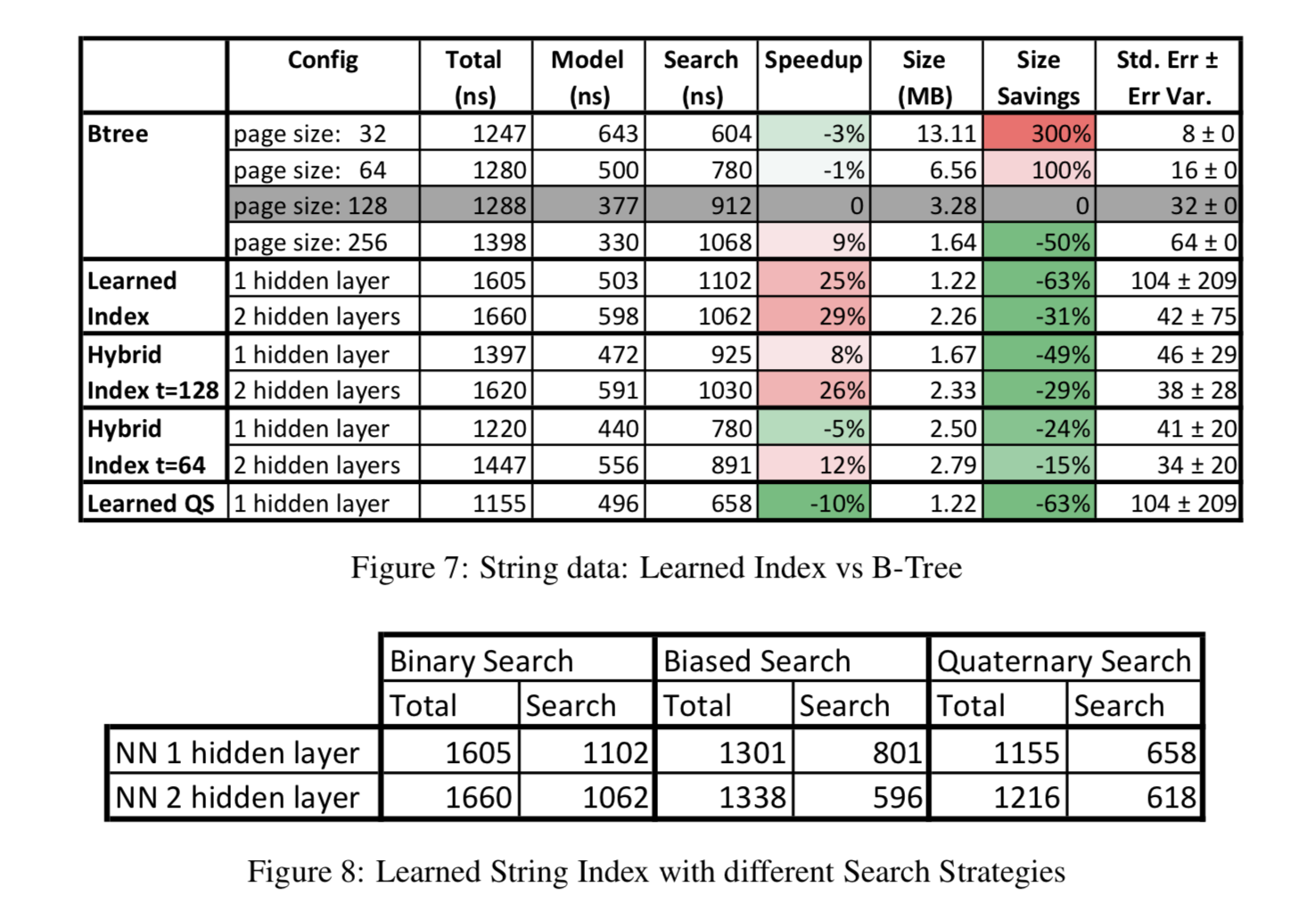
总的来说,在索引的内存占用上大大有了显著减少。在索引时间上,在特定的配置下也能有一些提升(最后一组实验比较有说服力,因为我们的初衷是找出人们发现不了数据特殊性)。可以看到,这里实验用的RMI只有两层,而且误差不稳定。猜想是如果更深的RMI,精度提出和时间效率提升以及内存占用提升相比并没有太好,当然未来可以进一步采样模型压缩来优化。
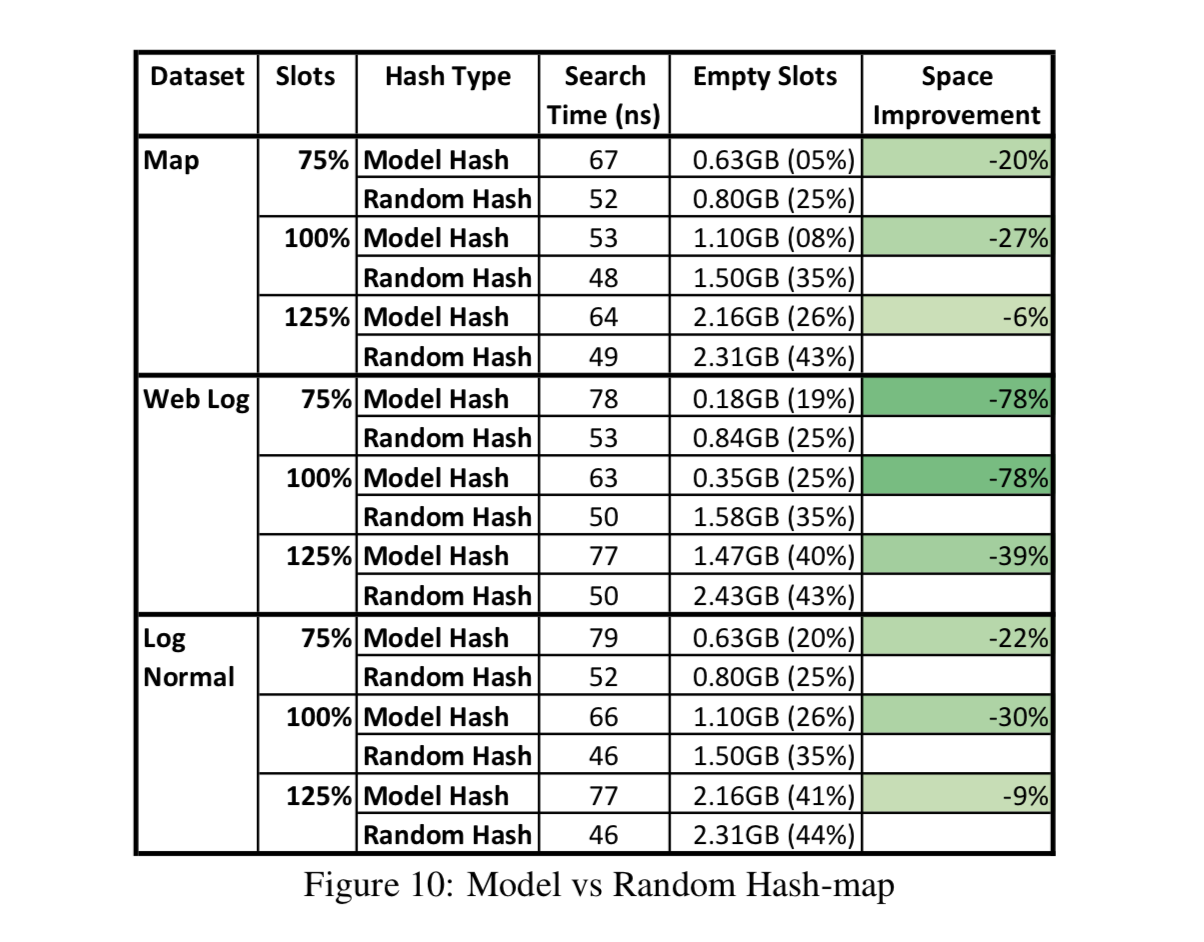
Point Index. Point Index顾名思义就是为了搜索出key对应的position,也就是Hashmap。Hashmap天然就是一个模型,输入是key输出是position。对于Hashmap来讲,为了减少冲突,往往需要使用比key本身数目大很多的slots数目(论文中提到在Google通常一个hashmap有78%额外的slots)。对于冲突,虽然有linked-list或者secondary probing的方式来处理,但是它们的开销都不算小。即使用sparse-hashmap的方式来优化内存占用,性能也要比hashmap慢3-7倍。因此能否通过学习出的模型一方面来减少额外内存开销的,另一方面减少一些冲突时的开销(Hashmap可以通过用更多的slots数目来避免冲突,如果冲突很少就很再难优化索引时间因为Hashmap本来就是常数复杂度的,所以说到底这里的目标是在保证索引时间的情况下减少Hashmap的内存开销)。如下图所示,Learned Hashmap可以在slots数目一样多的条件下既减少冲突,也就能更好地利用内存空间。
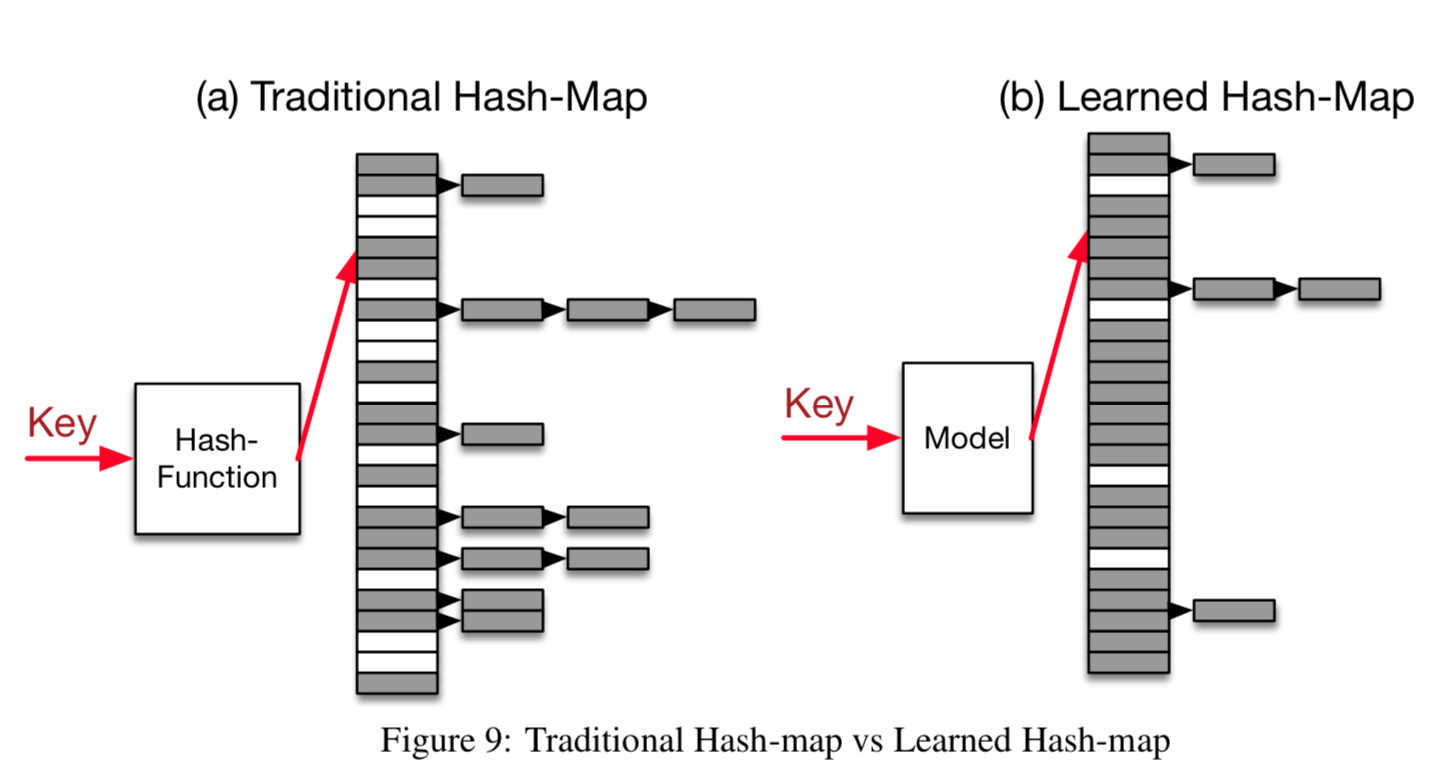
文中通过实验验证了拟合累计分布函数CDF对学习Hashmap也起作用:\(h(Key) = F(Key) * M \),其中想训练处F去拟合数据的CDF函数。由于point index不需要保证records连续(不需要考虑maxerr和minerr),所以训练出的模型F拟合CDF更容易得到满足。如果这时仍有少量的冲突,可以用linked-list的方式来处理。下图给出了实验结果,仍然使用了B-Tree实验中的Map、Weblog和LogNormal数据集以及两层都是线性experts的RMI模型(最底层100K个experts)。结论是learned index能达到更少的(~80%)empty slots而搜索时间和原本Hashmap相近,这大大地提高了内存使用率。同样,若learned index不能很好地学出CDF(比如冲突很多),系统可以rollback到Hashmap。
Existence Index. 对于Existence Index,DBMS采样Bloom-Filter来实现:对于一个key,算出k个hash函数得到的在bit array上的position并标记成1。Bloom-Filter能天然杜绝false negatives的存在,但有false positive的存在。为了降低false positive,比如对于一个100M记录的数据,Bloom-Filter通常需要比records本身大14倍的bits来达到0.1%的false positive准确度。
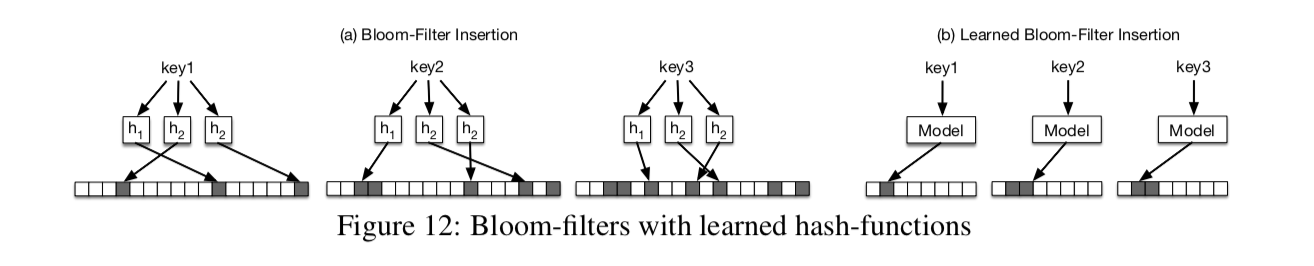
这里learned index目标和之前讨论的B-Tree及Hashmap都不一样。之前我们想学习出现有的keys里的分布规律,而这里对于存在的keys我们却不需要区别对待。相反,我们想通过模型学出存在的keys和不存在的keys间的差异。换句话讲,如上图所示,我们期望存在的keys对应索引的positions尽量在一起(无所谓冲突不冲突),不存在的keys对应索引的positions尽量在一起,而存在key和不存在key索引出来的position尽量分开。同时,learned index应该满足尽量低的FPR和内存占用且保证FNR为0。
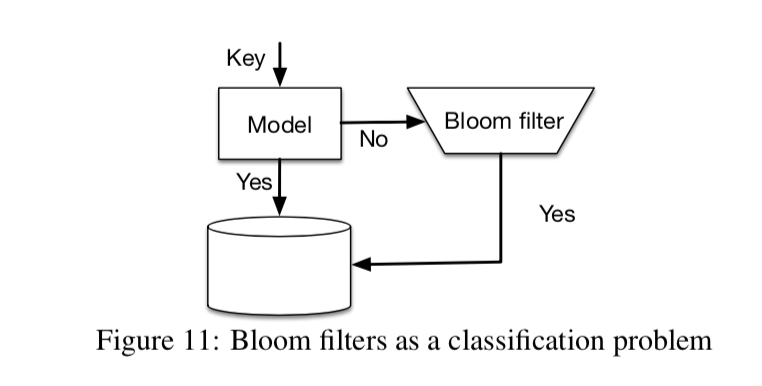
论文中提出了两种思路来建模,来满足上述要求。第一种方式可以把existence index看成是一个binary classification问题。考虑到existence index的使用场景通常是先判断record在cold storage存不存在,再通过disk或网络access数据。所以latency相对可以高一些,这样我们就可以用更复杂的RNN或CNN模型来当做分类器了。在预测的时候,模型会得到输入key是存在的可能性,需要给定一个threshold(τ)来做出实际判断。然而,这样训练出来的不同模型有其对应的FNR和FPR。我们可以通过threshold来降低FPR,但FPR降低FNR会增加,因为对于一个训练好的模型,调整τ整个False Rate是不变的(FR = FPR+FNR),这破坏了系统的Semantic Guarantees。论文解决的思路非常简单:对于模型要给出negative预测的keys,借助(rollback)传统的bloom filter来保证这个特性。由于这时的bloom filter只对< threshold的数据建,因此总体来说learned index可以很好地优化内存。即使FNR = 50%,理论上我们可以把内存优化到一半(类似Amdahl’s Law)。这样一来, threshold的选取就只需要考虑FPR了。
第二种方式,还是把问题看成一个binary classification问题。训练得到了模型f以后,因为它满足不了FNR=0,我们可以把f来代替Bloom-Filter中的hash函数:\( d(f(key)) = m * f(key) \),其中m是bit array的大小。用这样的函数做成的bloom-filter可以大大减少bit array的大小。可以看到,两种方式都把上一段提到的目标当成一个binary classification问题,然后为了Semantic Guarantees,都是结合Bloom-filter本身来实现的,只是在不同level的hybird。
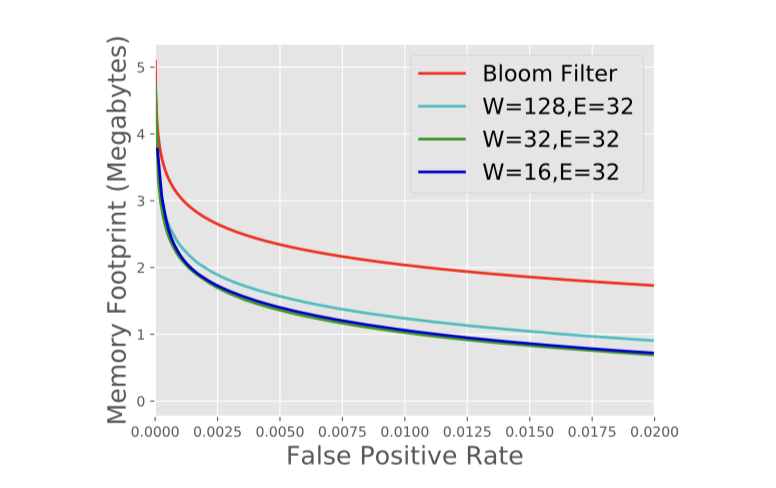
对于Existence Index,论文用了Google内部的1.7M个钓鱼网站URL当成是存在的key,把合法的URL当成是不存在的key,模型用了GRU。下图给出了在不同GRU配置下和不同FPR的threshold下的结果。实际上,相比B-Tree和Hashmap,这里实验给出的内存优化效果是比较明显的。并且模型预测越准确,内存降低地越明显,但这里论文中没有给出性能对比。
回到本文最开始提到的四个问题。我们已经通过例子讨论了如何解决Semantic Guarantees和Evaluate Efficiency。那么learned index如何处理Overfitting和No Specialization问题呢?对于overfitting,论文的假设是要被新索引的key依然满足CDF。比如对于Learned Range Index的 insert操作,如果新的key也同样来源于训练出的CDF分布,那么我们并不需要重新训练,直接insert到预测出来的position就行了。而B-Tree则需要O(log N)甚至re-balance。但RMI解决the last-mile accuracy的方式决定了learned index并不能很好地generalize,这是可以进一步完善的地方。而对于No Specialization的数据索引,虽然learned index并不能generalize,但能在当前情况下提高查询效率,减少内存使用。对于OLAP为主的系统,更新索引的操作本来就是定期进行,可以这时再重新训练模型,这时训练的初值可以使用之前训练出来的权重。如果OLTP数据更新更频繁的系统,可以采用delta-index的一些技术,增量地更新learned index。文中还提到当CDF分布变化时的模型处理,这里不展开介绍了,详见3.7.1。另外对于面向disk索引的数据库系统来说,逻辑页并不是真正的物理页(从而不能满足前文分析的性质),论文中也给出了几个可能可行的方式优化,详见3.7.2。
说来巧合,其实类似的问题去年和同事讨论过。在Pivotal的时候,我和几个同事结合ML和DB做过一些尝试,比如用SQL写推荐系统,通过Transaction Log检测作弊用户和异常行为并集成到查询层。也经常讨论,如果用数据库系统去实现深度学习,可行吗?有哪些优势?我们从存储,计算,表达问题的泛化能力等几方面讨论过很多次,但每次都没有很好地去切入。现在想来,有点惭愧,因为我当时更关注的是如何用数据库里的一些技术做ML,而不是如何用ML来优化数据库设计。一次,明哥问我能不能用ML尝试优化plan,减少查询次数,能否对各类的join做些优化。我们讨论到索引优化,但遗憾的是当时并没有深入。不过,就像paper里所断言的,this is a fruitful direction for future research。
Hong Wu at 20:00

